Preface
- The consensus problem
- Consensus with Byzantine Failures
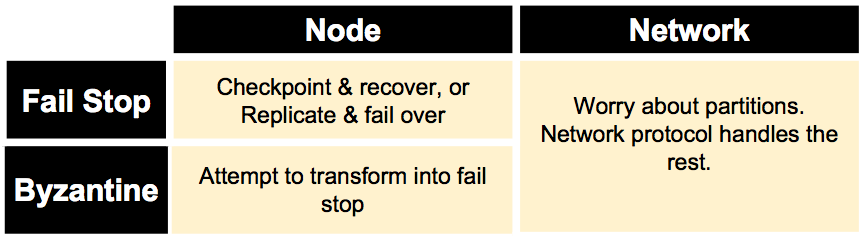
Processor Failures in Message Passing
Fail stop: at some point the processor stops taking steps- at the processor’s final step, it might succeed in sending only a subset of the messages it is supposed to send, e.g.:
Crash- Power outage
- Hardware failure
- Out of memory/disk full
- Strategies:
- Checkpoint state and restart (High latency)
- Replicate state and fail over (失效备援) (High cost)
- at the processor’s final step, it might succeed in sending only a subset of the messages it is supposed to send, e.g.:
Byzantine: Everything that is not fail stop. Processor changes state arbitrarily and sends message with arbitrary content.- E.g.:
- Bit flip in memory or on disk corrupts data
- Older version of code on one node sends (now) invalid messages
- Node starts running malicious version of software
- Goal: turn into fail stop
- Checksums/ECC (Error Correction Code)
- Assertions
- Timeouts
- E.g.:
Failure Matrix
Negative result for link failures
It is impossible to reach consensus in case of link failures, even in the synchronous case, and even if one only wants to tolerate a single link failure.
Consensus under link failures: the 2 generals problem.
- There are two generals of the same army who have encamped a short distance apart.
- Their objective is to capture a hill, which is possible only if they attack simultaneously.
- If only one general attacks, he will be defeated.
- The two generals can only communicate by sending messengers, which is not reliable.
- Is it possible for them to attack simultaneously?

See Fischer/Lynch/Paterson for more discussion.
The Consensus Problem
Each process starts with an individual input from a particular value set V. Processes may fail by crashing. All non-faulty processes are required to produce outputs from the value set V, subject to simple agreement and validity. A solution to the consensus problem must guarantee the following:
Termination: Eventually every nonfaulty processor must decide on a value (decision is irrevocable).Agreement: All decisions by nonfaulty processors must be the same.Validity: If all inputs are the same, then the decision of a nonfaulty processor must equal the common input
Once a processor crashes, it is of no interest to the algorithm, and no requirements are placed on its decision.
f-resilient system:
- at most
fprocessors may fail - The set of faulty processors may be different in different executions.
In the last round:
Clean crash: none or all of the outgoing messages are sentNot-clean crash: an arbitrary set of its outgoing messages are delivered.
Consensus algorithm in the presence of crash failures
Each process maintains a set of the values it knows to exist in the system; initially, this set contains only its own input. At the first round, each process broadcasts its own input to all processes. For the subsequent f rounds, each process takes the following actions:
- updates its set by joining it with the sets received from other
processes, and - broadcasts any new additions to the set to all processes.
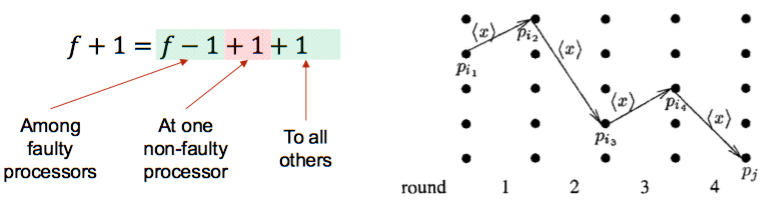
After f+1 rounds, the process decides on the smallest value in its set.

- Intuition for
Agreement: Assume that a process pi decides on a value x smaller than that decided by some other process p_j. Then, x has remained “hidden” from pj for (f+1) rounds. We have at most f faulty processes. A contradiction!!! - Number of processes: n > f
- Round Complexity: f + 1
- Message Complexity: (at most) n^2 * |V| messages, where V is the set of input values.
Worst case scenario
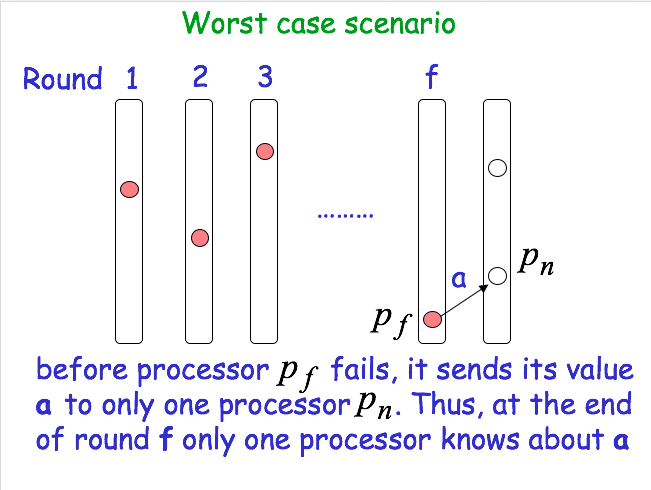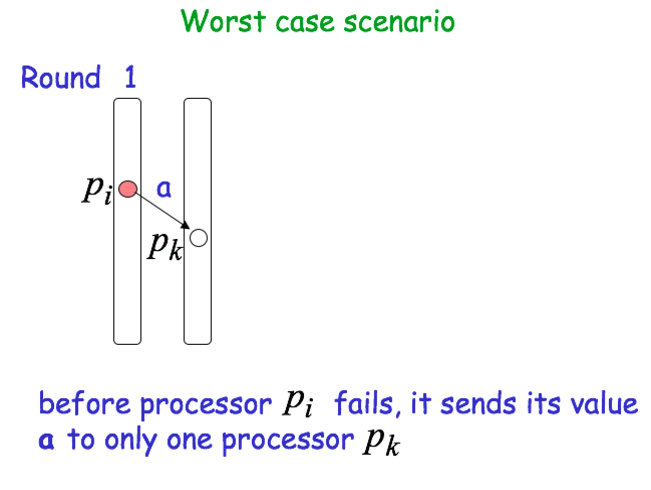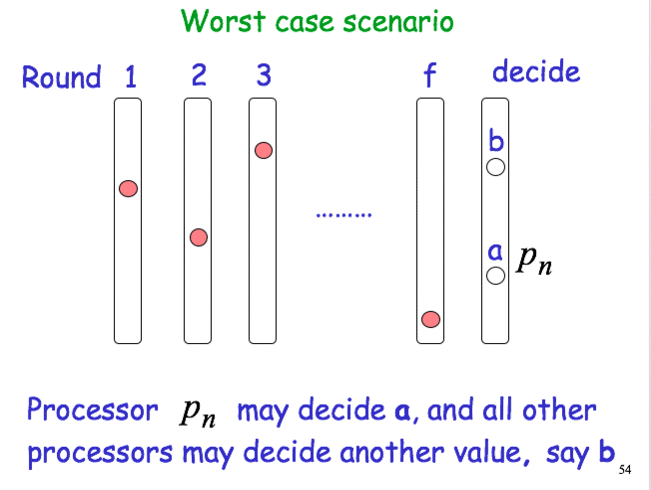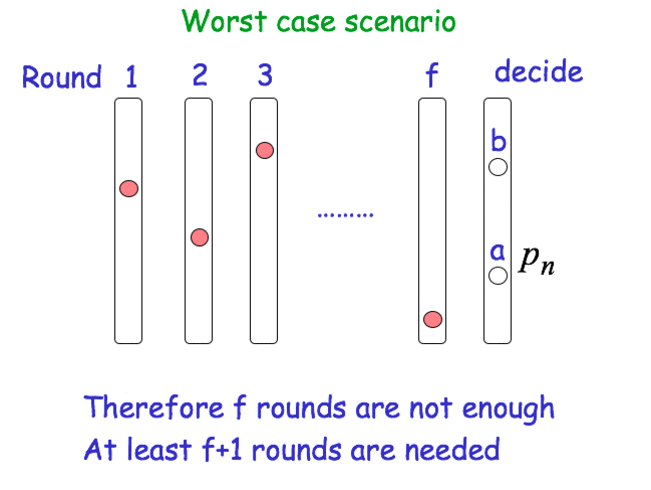
Consensus with Byzantine Failures
Theorem (5.7): Any consensus algorithm for 1 Byzantine failure must have at least 4 processors.
Proof of Theorem 5.7: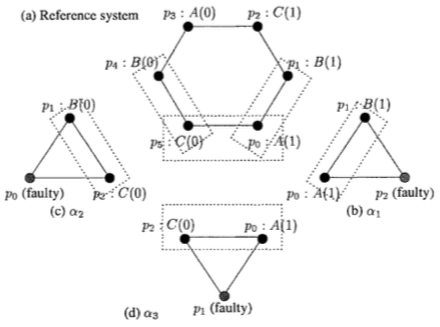
Theorem: Any consensus algorithm for f Byzantine failures must have at least 3f+1 processors.
- Partition the processors into three sets P0, P1, P2;
- Each containing at most n/3 processors
- P0 simulates p0, P1 simulates p1 and P2 simulates p2
- n processors solves consensus => {p0, p1, p2} solves consensus. ==> Contradiction.
Exponential Information Gathering (EIG) Algorithm
This algorithm uses
- f + 1 rounds (optimal)
- n = 3f + 1 processors (optimal)
- exponential size messages (sub-optimal)
Each processor keeps a tree data structure in its local state. Values are filled in the tree during the f + 1 rounds
At the end, the values in the tree are used to calculate the decision.
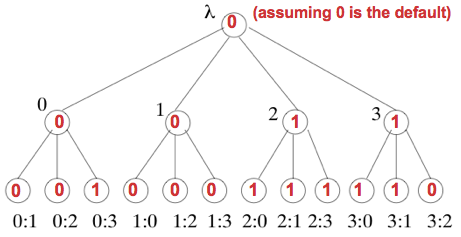
Local Tree Data Structure
- Each tree node is labeled with a sequence of unique processor indices.
- Root’s label is empty sequence ; root has level 0
- Root has
nchildren, labeled 0 through n - 1 - Child node labeled i has n - 1 children, labeled i : 0 through i : n-1 (skipping i : i)
- Node at level
dlabeledvhasn - dchildren, labeled v : 0 through v : n-1 (skipping any index appearing in v) - Nodes at level f + 1 are leaves.
The tree when n = 4 and f = 1 :
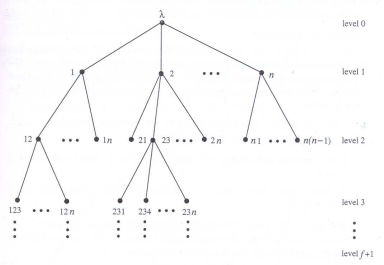
Filling in the Tree Nodes
- Initially store your input in the root (level 0)
- Round 1:
- send level 0 of your tree to all
- store value x received from each p_j in tree node labeled j (level 1); use a default if necessary
- “pj told me that pj ‘s input was x”
- Round 2:
- send level 1 of your tree to all
- store value x received from each pj for each tree node k in tree node labeled k : j (level 2); use a default if necessary
- “pj told me that pk told pj that pk’s input was x”
- Continue for f + 1 rounds
Calculating the Decision
- In round f + 1, each processor uses the values in its tree to compute its decision.
Recursively compute the “resolved” value for the root of the tree,
resolve(), based on the “resolved” values for the other tree nodes:
Example of resolving values when n = 4 and f = 1:
A Polynomial Algorithm (The King Algorithm)
We can reduce the message size to polynomial with a simple algorithm.
- The number of processors increases to: n > 4f
- The number of rounds increases to 2(f + 1)
- Uses f+1 phases, each taking two rounds.

Asynchronous Consensus
Assumptions
- Communication system is reliable
- Only processor failures (crash / Byzantine)
- Completely asynchronous
Theorem: For n ≥ 2, there is no algorithm in the read/write shared memory model that solves the agreement problem and guarantees wait-free termination
Consensus is impossible!!!
- Even in the presence of one single
processor (crash) failure
Proof of impossibility
- Impossibility for shared memory
- The (n-1)-resilient case (wait-free case)
- The 1-resilient case
- Impossibility for message passing
- Simulation
- Impossibility motivates the use of
failure detectors.- E.g., “The weakest failure detector for solving consensus”, JACM 43(4).
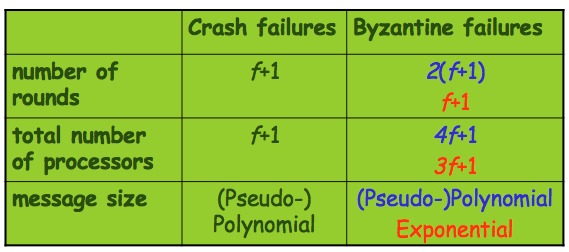
Summary
Let f be the maximum number of faulty processors.
References
[1] Attiya, Hagit, and Jennifer Welch. Distributed computing: fundamentals, simulations, and advanced topics. Vol. 19. John Wiley & Sons, 2004..
[2] Byzantine Fault Tolerance, Distributed System (A free online class), by Chris Colohan.
[3] The Byzantine Generals Problem, Leslie Lamport, Robert Shostack and Mashall Peace. ACM TOPLAS 4.3, 1982.
[4] CSCE 668: Distributed Algorithms and Systems Spring 2014.

