Preface
- The MUTEX problem
- the shared memory model
- problem definition
- The unbounded algorithm
- The bakery algorithm
- The unbounded algorithm
Shared Memory Model
Processes communicate via a set of shared variables (also called shared registers), each shared variable has a type, defining a set of primitive operations (performed atomically)
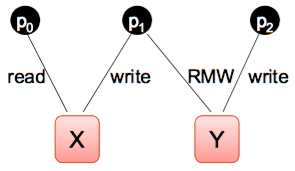
Several types of shared variable can be employed, e.g.
- read/write
- read-modify-write (RMW)
- compare&swap (CAS)
Each register has a type, which specifies:
- Values to be taken on by registers
- Operations performed on the registers
- Values to be returned by operations (if any)
- New values of the register resulting from the operation
A configuration in the shared memory model is a vector: C =
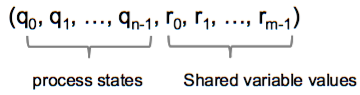
where q_i is a state of p_i and r_j is a value of register R.
The events in a shared memory system are:
- computation steps taken by the processors and are denoted by the index of the processor;
- At each computation step, the shared variable is accessed.
In asynchronous shared memory systems, an execution is admissible if each processor has an infinite number of computation steps.
Complexity measures
Obviously in shared memory systems there are no messages to measure. Instead we focus on the space complexity, the amount of shared memory needed to solve problems.
- Number of distinct shared variables required
- and the amount of shared space (e.g., # of bits)
Changes from the MSG model
- Communication medium changes
- No inbuf and outbuf state components
- Configuration includes values for shared variables
- Execution manner changes
- One event type: one computation step by a process
- pi’s state in old configuration specifies which shared variable is to be accessed and with which primitive
- shared variable’s value in the new configuration changes according to the primitive’s semantics
- pi’s state in the new configuration changes according to its old state and the result of the primitive
- One event type: one computation step by a process
The Mutual Exclusion Problem
Each processor’s code is divided into four sections:
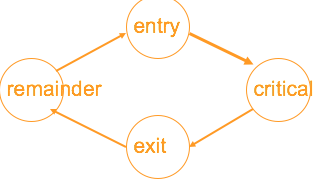
Entry (trying): the code executed in preparation for entering the critical sectionCritical: the code to be protected from concurrent executionExit(release): the code executed on leaving the critical sectionRemainder: the rest of the code
Each processor cycles through these sections in the order: remainder –> entry –> critical –> exit –> remainder.
An algorithm for a shared memory system solves the mutual exclusion problem with no deadlock (or no lockout) if the following holds (three properties):
Mutual exclusion: In every configuration of every execution, at most one processor is in the critical section.No deadlock: In every admissible execution, if some processor is in the entry section in a configuration, then there is a later configuration in which some processor is in the critical section.No lockout: In every admissible execution, if some processor is in the entry section in a configuration, then there is a later configuration in which that same processor is in the critical section.
Mutex progress conditions:
- no deadlock
- no lockout
bounded waiting: no lockout + while a processor is in its entry section, other processors enter the critical section no more than a certain number of times.
These three conditions are increasingly strong.
The code for the entry and exit sections is allowed to assume that:
- no processor stays in its critical section forever
- shared variables used in the entry and exit sections are not accessed during the critical and remainder sections
Mutual Exclusion Using Powerful Primitives
We will show that
- one bit suffices for guaranteeing mutual exclusion with no deadlock
- while O(logn) bits are necessary (and sufficient) for providing stronger fairness properties.
Binary Test&Set Registers
The test&set operation atomically reads and updates the variable.

There is a simple mutual exclusion algorithm with no deadlock that uses one test&set register(Algorithm 7).

- One processor could always grab V (i.e., win the test&set competition) and starve the others.
- No Lockout does not hold.
- Thus Bounded Waiting does not hold.
Read-Modify-Write Registersz
The RMW operation read-modify-write all in one atomic operation.
Clearly, the test&set operation is a special case of rmw, where f(V) = 1 for any V.

Detailed analysis about algorithm 8 please refer to the textbook.
Mutual Exclusion Using Read/Write Registers
The Bakery Algorithm
Basic idea:
- Tell others “I want to enter the critical section”
- Get tickets and wait for my turn
We employ the following shared data structures:
Number: an array of n integers, which holds in its ith entry the number of p_iChoosing: an array of n Boolean values; Choosing[i] istruewhile p_i is in the process of obtaining its number.
Because several processors can read Number concurrently it is possible for several procesors to obtain the same number!.
To break symmetry, we define p_i's ticket be the pair (Number[i], i) (uniqueness)(tickets之间的序比较可以使用字典序).

Algorithm 10 provides mutual exclusion and no lockout. (proof pls refer to the textbook)
The numbers can grow without bound, unless when every processor is in the remainder section.
How to achieve MUTEX when variables have finite size.
A Bounded Mutual Exclusion Algorithm for 2 Processors
Algorithm 11 provides mututual exclusion and no deadlock for two processors p_0 and p_1. Each processor p_i has a Boolean shared variable Want[i].
- Want[i]=1: if p_i wants to enter the critical section.
However, the algorithm gives prioirty to one of the processors and the other one can starve.

We then convert this algorithm to one that provides no lockout as well.
To achieve no lockout, we modify the alrgorithm so that instead of always giving priority to p_0, each processor gives priority to the other processor on leaving the critical section.
Priority: Shared variable, contains the id of the processor that has the priority at the moment.
In the entry, wait until:
- Case 1: the other processor has the priority (but does not want to enter the critical section)
Case 2: I have the priority.

A Bounded Mutual Exclusion Algorithm for n Processors (recursively use the [2, no lockout] algorithm)
To construct a solution for the general case of n processors we employ the algorithm for two processors.
- Proceessors compete pairwise, using the two-processor algorithm described above, in a
tournament tree(锦标赛树) arrangement. - The pairwise competitions are arranged in a complete binary tree.
- Each processor begins at a specific leaf of the tree.
- At each level, the winner gets to proceed to the next higher level, where it competes with the winner of the competition on the other side of the tree.
- The processor that wins at the root enters the critical section.
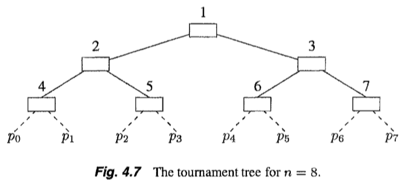
v: node number; we associate shared variableWant^v[0],Want^v[1], andPriority^v(all initialized to 0)To begin the competition for the (real) critical section, processor
p_iexecutesNode(2^k + i/2, i mod 2)- note that the leaves of the tree are numbered 2^k, 2^k + 1, …, 2^(k+1) - 1 (see Fig. 4.7).
the processor on the left (right) side play the role of p_0 (p_1)


