- Discuss the leader election (LE) problem in message-passing systems for a ring topology, in which a group of processors must choose one among them to be a leader.
- Present the different algorithms for leader election problem by taking the cases like anonymous/non-anonymous rings, uniform/non-uniform rings and synchronous/asynchronous rings etc.
[Based on the book “Distributed Computing“ by Hagit attiya & Jennifer Welch]
Ring Networks
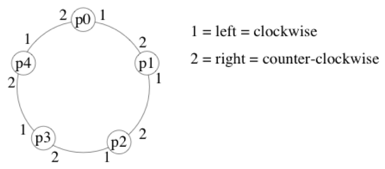
- In an
oriented ring, processors have a consistent notion of left and right.- For example, if messages are always forwarded on
channel 1, they will cycle clockwise around the ring.
- For example, if messages are always forwarded on
Why study rings?
- simple starting point, easy to analyze
- abstraction of a token ring
- lower bounds and impossibility results for ring topology also apply to arbitrary topoligies.
The Leader Election (LE) Problem
- LE problem is for each processor to decide that either it is the leader or non-leader, subject to the constraint that exactly one processor decides to be the leader.
- LE problem represents a general class of symmetry-breaking problems.
- For example, when a
deadlockis created, because of processors waiting in a cycle for each other, the deadlock can be broken by electing one of the processor as a leader and removing it from the cycle.
- For example, when a
- Each processor has a set of
elected (won)andnot-elected (lost)states. - Once an elected state is entered, processor is always in an elected state (and similarly for not-elected): i.e., irreversible decision.
- In every admissible execution:
- every processor eventually enters an elected or a not-elected state
- exectly one processor (the
leader) enters an elected state.
Uses of LE
- A leader can be used to coordinate activities of the system:
- find a
spanning treeusing the leader as the root; - reconstruct a
lost tokenin a token-ring network.
- find a
Uniform (Anonymous) Algorithms
Anonymous or not: A leader election algorithm is anonymous if processors do not have unique identifiers that can be used by the algorithm- Message recipients can only be specified in terms of channel labels, e.g., left and right neighbors
- ==> Every processor in the system has the same state machine.
- A
uniformalgorithm does not use the ring size (same algorithm for each size ring)- Formally, every processor in every size ring is modeled with the same state machine
- Uniform: since the algorithm looks the same for every value of n.
- A
non-uniformalgorithm uses the ring size (different algorithm for each size ring)- Formally, for each value of n, every processor in a ring of size n is modeled with the same state machine An .
Leader Election in Anonymous Rings
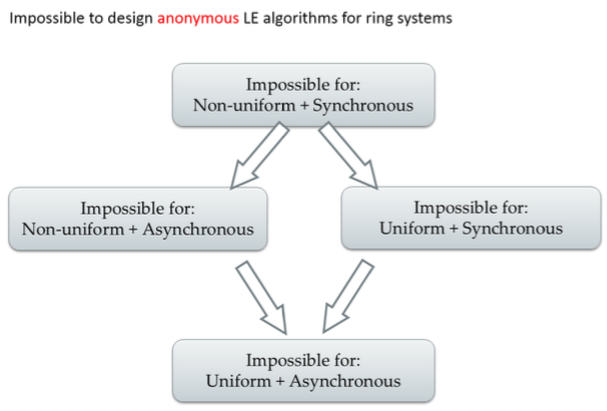
Theorem: For nonuniform algorithms and synchronous rings, there are no anonymous LE algorithms.
Proof Sketch:
- Every processor begins in same state with same outgoing msgs (since anonymous)
- Every processor receives same msgs, does same state transition, and sends same msgs in round 1
- Ditto for rounds 2,3,…
- Eventually some processor is supposed to enter an elected state. But then they all would.
Proof sketch shows that either safety (never elect more than one leader) or liveness (eventually elect at least one leader) is violated. Since the theorem was proved for non-uniform and synchronous rings, the same result holds for weaker (less well-behaved) models (uniform / asynchronous).
Lattice) (格)
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every two elements have a unique supremum (上确界) (also called a least upper bound or join, a ∧ b) and a unique infimum (下确界)(also called a greatest lower bound or meet, a V b)
Based on the impossibility result, we can reasonably assume that: Rings with unique processor identifiers.
LE in Asynchronous Rings
There exists algorithms when nodes have unique ids. We will evaluate them according to their message complexity.
Brute Force LE
Analysis
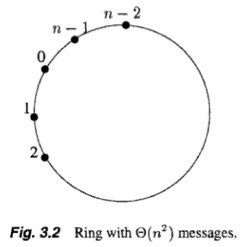
- Correctness: Elect processor with the largest id. (Time: O(n))
- Message complexity: Depends on how the ids are arranged.
- largest id travels all around the ring (n msgs)
- 2nd largest id travels until reaching largest
- 3rd largest id travels until reaching largest or second largest.
- etc.
- Worst way to arrange the ids is in decreasing order (Fig.3.2)
The O(n^2) algorithm is simple and works in both sync and async model. But how to optimize?
Idea: try to have message containing smaller ids travel smaller distance in the ring.
k-neighbour Forwarding
- Basic idea
- Gradually increase the scope of sending
- Eliminate unnecessary senders accordingly
- Smaller IDs are swallowed
- Clever forwarding
- k-neighbourhood
- 2k+1 nodes: k left + k right + self
- in the kth phase, LE among the 2^k-neighborhood
- size of neighbourhood doubles in each phase
- only the winner survives to the next phase
- k-neighbourhood

Analysis
- Correctness: similar to O(n*2) algorithm
- Message complexity
- Each msg belongs to a particular phase and is initiated by a particular proc.
- Probe distance in phase k is 2^k
- Number of msgs initiated by a proc. in phase k is at most 4 * 2^k (probes and replies in both directions)
- How many proc. initiate probes in phase k ?
- For k = 0, every proc. does
- For k > 0, every proc. that is a “winner” in previous phase (phase k-1) does
- Maximum number of phase k-1 winners occurs when the are packed as densely as possible:
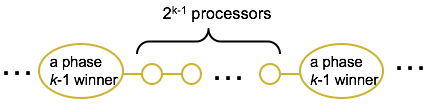
- Total number of phase k-1 winners is at most n/(2^(k-1) + 1)
- How many phases are there?
- let n/2^(k-1) + 1 == 1 (at the last phase there exists only one winner) ==> k = log(n-1) + 1 = number of phases
So the total number of msgs is sum, over all phases, of number of winners at that phase times number of msgs originated by that winner: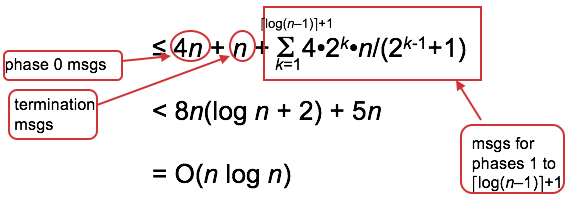
The O(log n) algorithm is more complicated than the O(n^2) algorithm but uses fewer messages in worst case.
Lower bound for LE Algorithm
Can we do better than O(nlogn) ?
Theorem: Any leader election algorithm for asynchronous rings whose size is not known a priori has Ω(nlog n) msg complexity (holds also for undirectional rings).
- The two algorithms above are comparison-based algorithms, i.e. they use the identifiers only for comparison (<, >, =)
- In synchronous networks, O(n) msg complexity can be achieved if general arithmatic operations are permitted (non-comparison based) and if time complexity is unbounded.
References
[1] Attiya, Hagit, and Jennifer Welch. Distributed computing: fundamentals, simulations, and advanced topics. Vol. 19. John Wiley & Sons, 2004.
[2] 分布式算法(黄宇)课程主页
[3] Distributed System

