- Broadcast / convergecast on a spanning tree
- Async / sync flooding to construct a spanning tree
- distributed DFS with/without a specific root
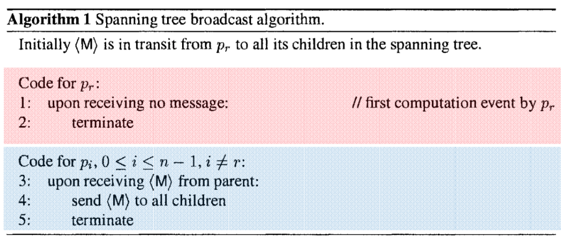
Broadcast over a rooted spanning tree
- Broadcast is used to send the information to all.
- Suppose processors already have information about a rooted spanning tree of the communication topology
- tree: connected graph with no cycles
- spanning tree: contains all processors
- rooted: there is a unique root node
- Implemented via
parentandchildrenlocal varialbes at each processor.- indicate which incident channnels lead to parent and children in the rooted spanning tree.
Spanning Tree: A tree is a connected undirected graph with no cycles. It is a spanning tree of a graph G if it spans G (that is, it
includes every vertex of G) andis a subgraph of G(every edge in the tree belongs to G). A spanning tree of a connected graph G can also be defined as a maximal set of edges of G that contains no cycle, or as a minimal set of edges that connect all vertices.
Complexity analysis:
- Synchronous model
- Time complexity: time is depth
dof the spanning tree. (at mostn-1when chain) - MSG complexity: number of messages is
n-1, since one message is sent over each spanning tree edges.
- Time complexity: time is depth
- Aysnchronous model
- Same as synchronous model.
Convergecast (from leaves to the root)
- Convergecast is used to collect the information.
- Again, suppose a rooted spanning tree has already been computed by the processors
- parent and children variables at each processor
- Do the opposite of broadcast
- leaves send msgs to their parents.
- non-leaves wait to get msgs from each child, then send combined (aggregate) info to parent.
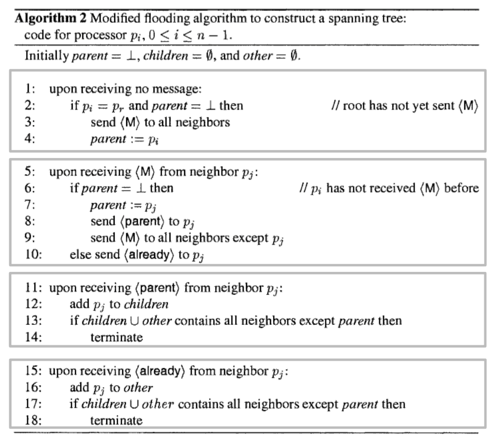
Finding a Spanning Tree Given a Root by Flooding
Flooding): Flooding is a simple computer network routing algorithm in which every incoming packet is sent through every outgoing link except the one it arrived on.
- root send M to all its neighbours
- when non-root first gets M,
- set the sender as its parent
- send “parent” msg to sender
- send M to all other neighbours (if no other neighours, then terminate)
- when get M otherwise,
- send “reject” to sender.
- use “parent” and “reject” msgs to set children varialbes and know when to terminate (after hearing from all neighbours)
Execution of spanning tree algorithm
- In the synchronous model: always gives breadth-first search (BFS) tree.
- Asynchronous: not necessarily BFS tree.
Both models achieves O(m) messages complexity and O(diam) time complexity.
Diameter
Dof a network is defined as the longest path of the shortest paths between any two nodes.
Distributed DFS with a Specified Root
- Basic rationale: sequential execution over a distributed system (of multiple processors)

Distributed DFS without a Specified Root
- Assume the processors have unique identifiers (otherwise impossible!)
- Idea:
- Each processor starts running a copy of the DFS spanning tree algorithm, with itself as root
- tag each msg with initiator’s id to differentiate
- when copies “collide”, copy with
larger id wins.
- Message complexity: O(n*m)
- Time complexity: O(m) (m: edges in graph)

References
[1] Attiya, Hagit, and Jennifer Welch. Distributed computing: fundamentals, simulations, and advanced topics. Vol. 19. John Wiley & Sons, 2004.
[2] 分布式算法(黄宇)课程主页
[3] Distributed System


