L02-Basic Message Passing Algorithms

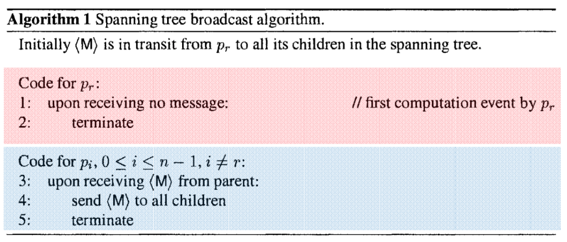
Broadcast / convergecast on a spanning tree
Async / sync flooding to construct a spanning tree
distributed DFS with/without a specific root

Broadcast over a rooted spanning tree

Broadcast is used to send the information to all.
Suppose processors already have information about a rooted spanning tree of the communication topology
- tree: connected graph with no cycles
- spanning tree: contains all processors
- rooted: there is a unique root node
Implemented via parent and children local varialbes at each processor.
- indicate which incident channnels lead to parent and children in the rooted spanning tree.

Spanning Tree: A tree is a connected undirected graph with no cycles. It is a spanning tree of a graph G if it spans G (that is, it includes every vertex of G) and is a subgraph of G (every edge in the tree belongs to G). A spanning tree of a connected graph G can also be defined as a maximal set of edges of G that contains no cycle, or as a minimal set of edges that connect all vertices.

Complexity analysis:

Synchronous model
- Time complexity: time is depth d of the spanning tree. (at most n-1 when chain)
- MSG complexity: number of messages is n-1, since one message is sent over each spanning tree edges.
Aysnchronous model
- Same as synchronous model.

Convergecast (from leaves to the root)

Convergecast is used to collect the information.
Again, suppose a rooted spanning tree has already been computed by the processors
- parent and children variables at each processor
Do the opposite of broadcast
- leaves send msgs to their parents.
- non-leaves wait to get msgs from each child, then send combined (aggregate) info to parent.

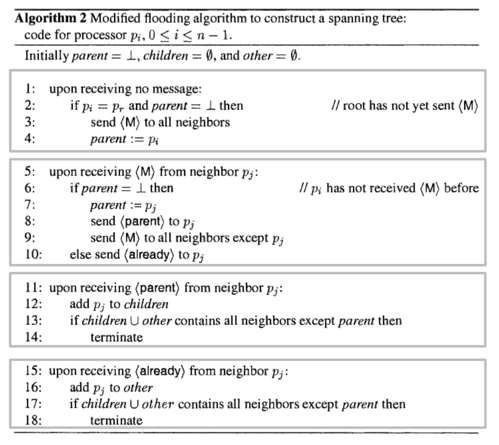
Finding a Spanning Tree Given a Root by Flooding

Flooding): Flooding is a simple computer network routing algorithm in which every incoming packet is sent through every outgoing link except the one it arrived on.

root send M to all its neighbours
when non-root first gets M,
- set the sender as its parent
- send “parent” msg to sender
- send M to all other neighbours (if no other neighours, then terminate)
when get M otherwise,
- send “reject” to sender.
use “parent” and “reject” msgs to set children varialbes and know when to terminate (after hearing from all neighbours)

Execution of spanning tree algorithm

In the synchronous model: always gives breadth-first search (BFS) tree.
Asynchronous: not necessarily BFS tree.

Both models achieves O(m) messages complexity and O(diam) time complexity.

Diameter D of a network is defined as the longest path of the shortest paths between any two nodes.

Distributed DFS with a Specified Root

Basic rationale: sequential execution over a distributed system (of multiple processors)

Distributed DFS without a Specified Root

Assume the processors have unique identifiers (otherwise impossible!)
Idea:
- Each processor starts running a copy of the DFS spanning tree algorithm, with itself as root
- tag each msg with initiator’s id to differentiate
- when copies “collide”, copy with larger id wins.
Message complexity: O(n*m)
Time complexity: O(m) (m: edges in graph)